Джон Уик, Корова, Водопой: как «отзеркалить» задачу, которую не решить в лоб

Взгляните на эту картинку. Самый эффективный киллер в мире,
человек-суперкомпьютер, сидит в меланхоличной позе рядом с коровой. Абсурд? Не
совсем. Это иллюстрация к гениальной задаче на смекалку, которая доказывает:
иногда, чтобы найти кратчайший путь, нужно посмотреть на мир из Зазеркалья. Это
не просто школьная геометрия, это настоящий тест на нестандартное мышление.
Давайте попробуем его пройти.

Проблема: Ахиллесова пята перфекциониста

Итак, легенда гласит: на время отойдя от дел, Джон Уик
занялся фермерством. Каждое утро его ритуал был прост: выйти из дома (точка А),
дойти до реки, набрать ведро воды и отнести его в хлев к любимой корове (точка
Б). Будучи гением оптимизации, Джон быстро понял, что его ежедневные маршруты
хаотичны и неэффективны. Его внутренний перфекционист требовал найти
единственно верный, кратчайший путь.

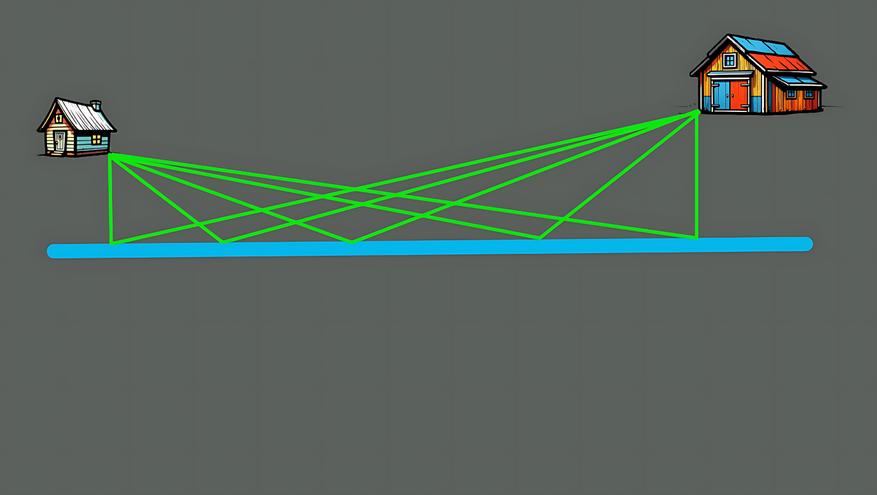
На первый взгляд, задача кажется тривиальной. Но очевидные
решения не работают:

• Идти по прямой от дома к хлеву? Корова останется без воды.
  Миссия провалена.

• Идти по прямой до реки, а затем по прямой к хлеву? Интуиция
  подсказывает, что угол имеет значение и это не всегда оптимально.

Как же супермозг Джона Уика должен был решить этот
логистический тупик?

Решение: Элегантный хак с «отражением»

А теперь — магия. Чтобы решить эту задачу, не нужно сложных
формул. Нужно совершить один мысленный трюк, который меняет всё.

Представим реку как прямую линию. А теперь сделаем то, что
кажется нелогичным: мысленно «отразим» хлев (точку Б) на противоположную
сторону реки, на то же расстояние от берега. Получим воображаемую точку Б’.

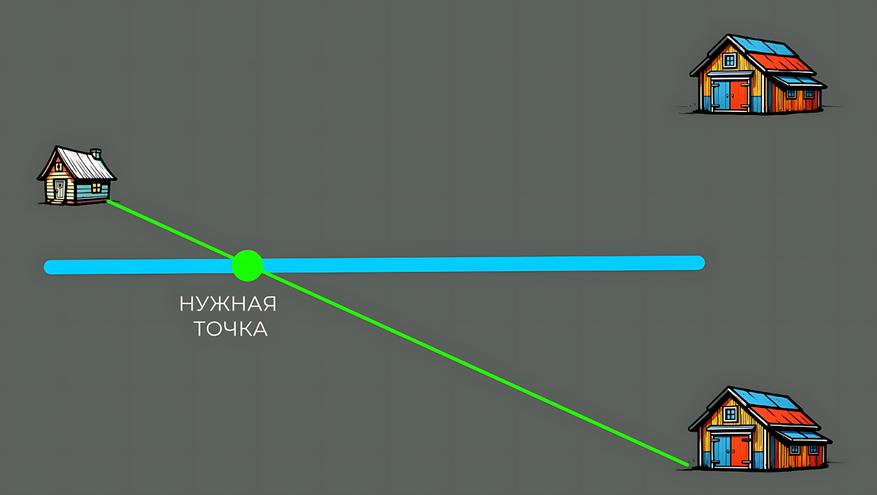
Почему это гениально? Потому что расстояние от любой точки
на реке до реального хлева (Б) теперь абсолютно равно расстоянию до нашего
воображаемого хлева (Б’).

И что это нам дает? А то, что теперь наша задача упростилась
до предела. Нам больше не нужно ломать маршрут у реки. Мы просто соединяем
прямой линией наш дом (А) и воображаемый хлев (Б’).

Точка, в которой эта прямая пересечет реку, и есть та самая
идеальная точка для водопоя.

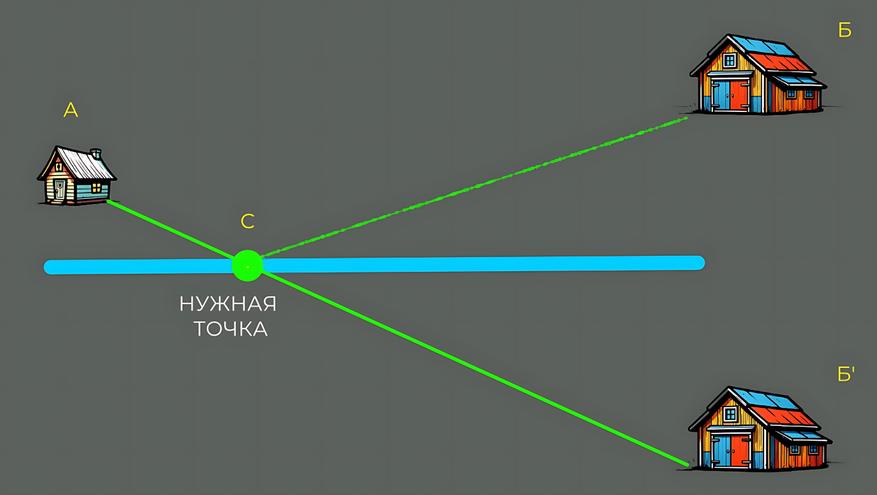
Путь «Дом → Идеальная точка на реке → Хлев» будет иметь ту
же длину, что и прямая «Дом → Воображаемый хлев». А поскольку прямая — это
кратчайшее расстояние между двумя точками, то и найденный нами маршрут — самый
короткий из всех возможных. Задача решена. Элегантно.

Вывод: Зачем это нужно знать не только Джону Уику

Эта задача — не про фермерство. Это блестящая метафора
решения сложных проблем. Когда вы заходите в тупик, пытаясь оптимизировать что-то
в рамках существующих условий, попробуйте применить «метод отражения»:

• Перенесите цель в другую плоскость. Посмотрите на нее под
  другим углом, создайте «воображаемый» аналог.

• Спрямите путь. Найдите самое простое и прямое решение для
  этой «отраженной» задачи.

• Вернитесь к реальности. Точка пересечения с вашей «рекой»
  (ограничением, проблемой) и будет самым эффективным решением в реальном мире.

Этот принцип работает в программировании при поиске
оптимальных алгоритмов, в бизнесе при построении логистических цепочек и даже в
быту, когда вы пытаетесь найти лучшее решение для сложной жизненной ситуации.
Иногда, чтобы найти выход, нужно просто посмотреть на мир вверх ногами. Или,
как в нашем случае, из-за реки.