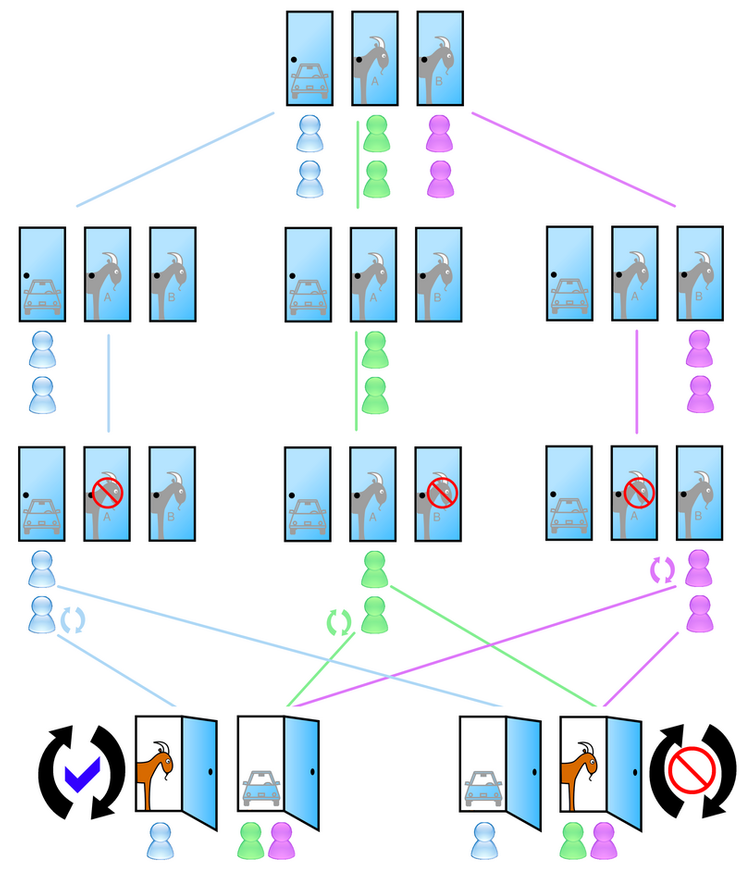
Представьте себе: вы стоите перед тремя дверями. За одной — автомобиль вашей мечты, за двумя другими — козы. Вы выбираете дверь, скажем, первую. В этот момент, ведущий шоу, обладающий волшебным знанием о том, где действительно находится автомобиль, открывает одну из оставшихся дверей, демонстрируя козу. Он предлагает вам выбор: остаться с вашей первой дверью или переключиться на другую, оставшуюся закрытой.
Кажется, что у вас равные шансы: 50 на 50, ведь автомобиль мог быть за любой из оставшихся дверей. Но интуиция обманчива. На самом деле, переключиться на другую дверь — это стратегически правильное решение, которое увеличивает шансы на выигрыш в два раза!
Это и есть знаменитый парадокс Монти Холла, который всколыхнул научный мир, породив споры, в которых участвовали даже самые выдающиеся умы. Эта простая игра, с ее удивительно контра-интуитивным решением, стала мощным инструментом для изучения человеческого мышления, демонстрируя наши слабые стороны в понимании вероятности и законов случайности.

Почему мы так упорно не хотим переключаться?
Основная причина кроется в том, что мы склонны рассматривать выбор Монти как случайное событие, не связанное с нашим первоначальным выбором. Мы привыкли к ситуациям, где каждый вариант имеет равные шансы, как при подбрасывании монеты или игре в кости. В таких случаях, даже после того, как срабатывает один из вариантов (например, выпадает шестерка на игральной кости), все варианты все равно остаются равновероятными при повторном подбрасывании.
Однако в парадоксе Монти Холла все иначе. Ведущий, обладая знанием, где находится автомобиль, не просто отбрасывает случайную дверь. Его выбор предоставляет вам дополнительную информацию — он «указывает» на дверь, где, скорее всего, находится коза. Оставаясь с первоначальным выбором, вы фактически игнорируете эту ценную информацию.

Переключение же означает, что вы доверяетесь знаниям ведущего и выбираете дверь, которая изначально имела два из трех шансов на победу.
Против богов и математиков
В 1990 году Мэрилин вос Савант, занесенная в книгу рекордов Гиннесса как обладательница самого высокого IQ в мире, в своей колонке «Спросите Мэрилин» объяснила правильный подход к парадоксу Монти Холла, опровергая устоявшиеся представления о равных шансах.
Ее ответ вызвал бурю негодования в научном сообществе. Математики, профессора, доктора наук написали ей тысячи писем, яростно споря с ее выводами. Среди них был даже известный математик Пол Эрдёш, который согласился с вос Савант только после того, как многократно проводил компьютерное моделирование игры.
Почему мы так упрямы?
Ответ кроется в глубинах нашего мышления. Мы склонны верить в то, что физическая реальность остается неизменной независимо от наших действий. Мы не замечаем, что знания ведущего, которое делает его подобным богу в этой игре, существенно меняет условия.
Парадокс Монти Холла — это не просто задача на вероятность. Это яркая иллюстрация того, как наша интуиция может быть обманчива, как недостаток критического мышления может вести к ошибочным суждениям, и как даже самые умные умы могут быть восприимчивы к логическим ловушкам.
Изучение мира через козлов
Парадокс Монти Холла стал основным элементом современной науки. Она используется в разных областях: от психологии до теории игр. Он позволяет нам глубоко погрузиться в противоречия между нашим интуитивным пониманием вероятности и ее строгими математическими основами.
Этот парадокс учит нас не бояться сомневаться в своих интуитивных суждениях, критически анализировать предлагаемые нам варианты и не бояться искать новые знания, которые могут изменить нашу картину мира.
