Мир, который мы видим, осязаем, ощущаем — это лишь вершина айсберга. Под поверхностью привычного скрывается квантовый мир, царство парадоксов и загадок. Здесь частицы ведут себя как волны, а волны — как частицы, время и пространство теряют свою привычную форму, а вероятность правит балом.

Квантовая механика, фундаментальная теория, описывающая микромир, разделяет физические явления на две категории: пертурбативные и непертурбативные. Пертурбативные явления, зависящие от постоянной Планка в простой форме, поддаются относительно легкому теоретическому описанию и экспериментальному наблюдению. Однако непертурбативные явления, такие как туннелирование, представляют собой значительную сложность для теоретического анализа.
Туннелирование — это квантовый эффект, при котором частица преодолевает потенциальный барьер, который в классической физике был бы непреодолим. Этот феномен лежит в основе таких процессов, как радиоактивный распад, ядерный синтез и работа туннельных диодов.
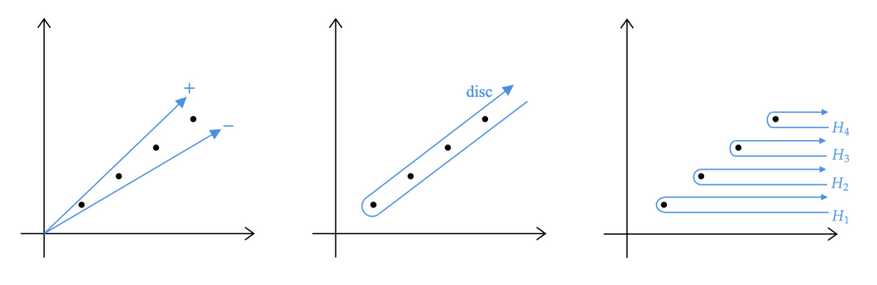
Исторически сложилось так, что описание туннельных явлений требовало различных математических подходов, что затрудняло создание единой теоретической основы для их изучения. Однако недавние исследования, опирающиеся на математический аппарат, разработанный Жаном Экалем в 1980-х годах, предлагают новый подход к унификации описания туннельных явлений.
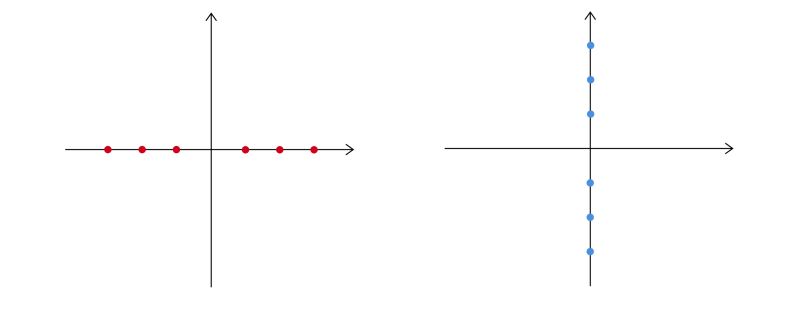
Центральным элементом этого подхода являются «трансряды» — обобщенные степенные ряды, включающие экспоненциальные и логарифмические члены. Трансряды позволяют представить волновую функцию частицы в виде суммы, где каждый член соответствует определенному пути туннелирования.
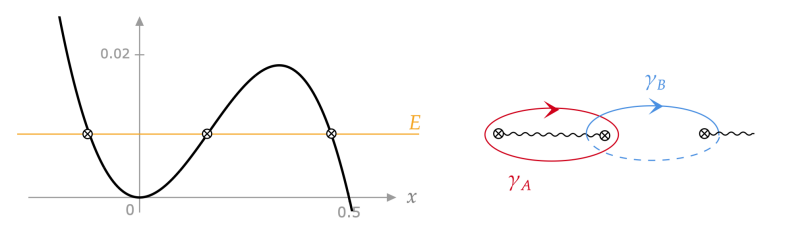
Применение трансрядов к анализу туннельных явлений обладает рядом преимуществ. Во-первых, это позволяет единообразно описывать различные типы туннелирования, независимо от формы потенциального барьера. Во-вторых, трансряды позволяют учесть явление Стокса — резкое изменение амплитуды туннелирования при изменении параметров системы. В-третьих, трансряды позволяют избежать неоднозначностей, связанных с традиционными методами вычисления непертурбативных эффектов.
Исследования ван Спаэндонка и Вонка показали, что трансряды, описывающие квантовое туннелирование, факторизуются на «минимальный» трансряд, отражающий базовые свойства туннелирования, и «медианный» трансряд, зависящий от конкретной задачи и отражающий специфические особенности системы.
Дальнейшие исследования в этом направлении могут быть направлены на изучение явления «пересечения стен» — изменения списка стабильных и нестабильных состояний системы при изменении параметров. Применение трансрядов к этой проблеме может привести к новым открытиям в области квантовой механики и ее приложений.
Таким образом, подход на основе трансрядов открывает новые перспективы для понимания и описания туннельных явлений в квантовой механике, что может иметь значительные последствия для развития различных областей науки и техники.
Если туннельный эффект настолько фундаментален, почему мы не наблюдаем его в макроскопическом мире?
Вероятность туннелирования экспоненциально уменьшается с увеличением массы частицы и ширины потенциального барьера. Поэтому для макроскопических объектов, таких как мяч или человек, вероятность туннелирования стремится к нулю.
Какие технологические применения может иметь туннельный эффект?
Туннельный эффект используется в различных устройствах, таких как туннельные диоды, сканирующие туннельные микроскопы, флэш-память и некоторые типы лазеров.

Является ли математическое описание туннелирования с помощью трансрядов единственно возможным?
Нет, существуют и другие методы описания туннелирования, например, метод WKB-приближения или метод интегралов по траекториям. Однако подход на основе трансрядов обладает рядом преимуществ, таких как универсальность и возможность учета тонких эффектов, таких как явление Стокса.
Может ли туннельный эффект быть использован для создания «телепортации» объектов?
В настоящее время нет научных оснований полагать, что туннельный эффект может быть использован для телепортации макроскопических объектов. Туннелирование — это квантовый эффект, который применим к микроскопическим частицам, и его вероятность для макроскопических объектов исчезающе мала.
Какие еще нерешенные проблемы связаны с туннельным эффектом?
Одной из таких проблем является полное понимание явления «пересечения стен» — изменения списка стабильных и нестабильных состояний системы при изменении параметров. Также остается открытым вопрос о том, как туннельный эффект влияет на динамику сложных квантовых систем.
